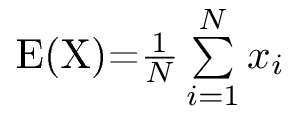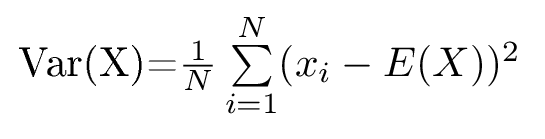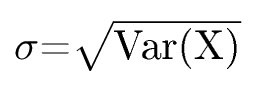Varianz & Standardabweichung – etwas Statistik für KMU

Sowohl Varianz als auch Standardabweichung sind Begriffe aus der Statistik. Statistisch fundiert können wir Vermutungen aussprechen, wie sich ein Ergebnis zusammen setzen wird oder klare Aussagen treffen, dass Werte mehr als normal abweichen. In diesem Zusammenhang nutzen wir Erwartungswerte, die Standardabweichung und die Varianz. Deswegen gehen wir diesen drei Begriffen im statistschen Umfeld dieses Beitrags auf den Grund.

Voraussichtliche Lesedauer: 12 Minuten

Warum sollten sich Selbständige und Unternehmer mit Varianz beschäftigen?

Um diese Frage zu Varianz und Standardabweichung zu klären, muss man zunächst wissen, was Statistik bedeutet:

Das Wort Statistik kommt vom lateinischen Wort statisticum, was den Staat betreffend bedeutet. Erst im 19. Jahrhundert wurde es im heutigen Sinne gebraucht: das allgemeine Sammeln und Auswerten von Daten.

Statistik beschäftigt sich mit der Erhebung und Auswertung von Daten. Ihr Ziel ist es, diese Informationen mit anderen Daten zu vergleichen oder Vorhersagen über die Entwicklung der Werte zu machen.

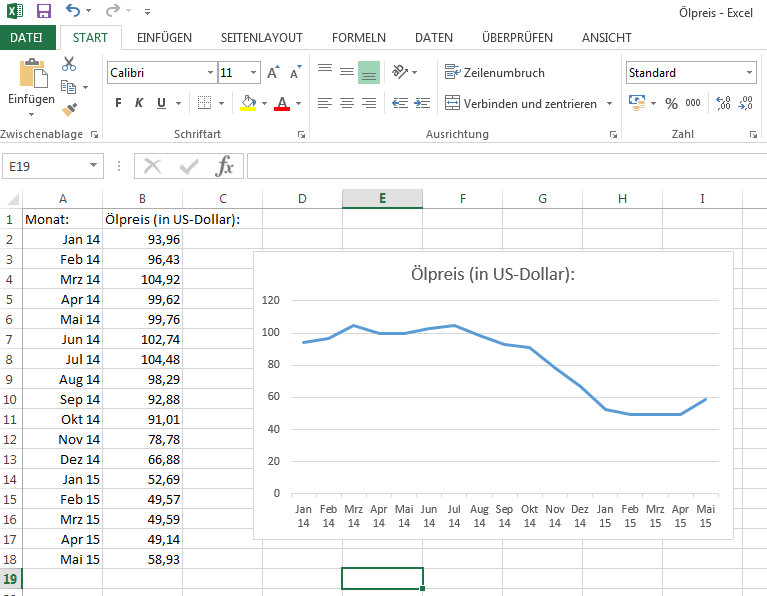
Diese Informationen können z.B. zur Veranschaulichung dienen. Ein Diagramm sagt beispielsweise mehr aus, als eine lange Liste von Zahlen nebendran, gerade wenn es um Varianz geht:

Diese Grafik zeigt die Ölpreis-Entwicklung von Januar 2014 bis Mai 2015. Man sieht deutlich den Fall des Ölpreises ab Mitte 2014. Anfang 2015 hat er sich stabilisiert und stieg daraufhin ab April 2015. Diesen Verlauf kann man anhand der Grafik viel besser erkennen als an blanken Zahlen.

Was kann man mit Varianz und anderen statistischen Mitteln in KMU herausfinden?

Statistik ist in kleinen Unternehmen vielseitig anwendbar, speziell in der Betriebswirtschaftslehre finden sich zahlreiche Anwendungen:

• betriebliche Kennzahlen ermitteln, um auch Vergleiche mit ähnlichen Unternehmen zu ermöglichen,
• Die Zahl der Reklamationen verschiedener Produkte zu ermitteln und zu vergleichen:
  • um Erkenntnisse über Qualität und Haltbarkeit von beispielsweise Baumaterialien zu gewinnen,
  • ob es sich lohnt teurere Materialien zu verwenden, wenn weniger Reklamationen anfallen (Vergleichsrechnung),
• Anwendungen in der Kostenrechnung (Festlegung eines Durchschnittspreises für Lagerbestände),
• Graphische Darstellungen sind hilfreich, um Entwicklungen besser zu verstehen,
• Vergleich zu Vorjahren (Preise, Rohstoffmenge, Gewinne, etc.).

Welche wichtigen statistischen Größen gibt es?

Es gibt viele statistische Größen, mit denen man Vorhersagen machen oder wichtige Informationen ermitteln kann. Da nicht alle für kleinere Unternehmen sinnvoll sind, beschäftige ich mich gezielt mit den wichtigsten und hilfreichsten für die oben genannten Anwendungen.

Der Erwartungswert

Was ist der Erwartungswert?

Führt man einen Versuch unendlich oft durch und bildet aus dem Ergebnis den (gewichteten) Mittelwert, erhält man den Erwartungswert. Das bedeutet dann in der Praxis, dass man beispielsweise eine gewisse Anzahl von Schrauben jeden Monat kauft. Eine kurze Aufgabe: Rechnen Sie alle Schrauben in einem Jahr zusammen und teilen Sie diese durch die Anzahl der Monate. Auf diese Art erhalten Sie den Erwartungswert für die Anzahl der gekauften Schrauben pro Monat.

Wo kommt der Erwartungswert vor?

Wie im obigen Beispiel beschrieben, kann man den Erwartungswert als Mittelwert über die verschiedensten Rohstoffe bilden. Damit kann man die durchschnittlich benötigten Materialien pro Monat oder Jahr ermitteln. Oder man berechnet über den gewichteten Mittelwert den Durchschnittspreis für einen Rohstoff, was bei der Festsetzung der Lagerkosten hilfreich sein kann. Man kann z.B. den durchschnittlichen Benzinpreis berechnen, um die Frachtkosten zu berechnen.

Für den Erwartungswert gibt es viele Einsatzmöglichkeiten, zum Beispiel im Rahmen der XYZ-Analyse.

Wie wird der Erwartungswert berechnet?

Der Erwartungswert wird in Berechnungen meistens als E(X) bezeichnet. Die Formel lautet:

Man sollte sich nicht von dieser Formel abschrecken lassen! Ihre Aussage ist, dass die einzelnen Werte (xi) zusammengezählt werden und dann durch die Anzahl der Daten (N) geteilt werden.

Praxisbeispiel zum Erwartungswert in Excel

Excel ermöglicht es uns noch einfacher mit dem Erwartungswert umzugehen! Die Formel MITTELWERT berechnet den Erwartungswert:

Dies ist unser Ölpreisbeispiel von oben, hier haben wir den Erwartungswert des Ölpreises für das Jahr 2014 berechnet.
Im oberen Teil des Bildes sieht man die Formel. Die blaue Umrandung zeigt an welche Werte (monatliche Ölpreise im Jahr 2014) für die Berechnung benutzt worden sind.

Der durchschnittliche Ölpreis für das Jahr 2014 beträgt 94,15 US-Dollar pro Barrel (Messeinheit für Öl).

Die Varianz und Standardabweichung

Definition Varianz und Standardabweichung: Was ist das?

Die Varianz und Standardabweichung sind ebenfalls wichtige Kenngrößen: sie geben die Größe der Abweichung vom Mittelwert an. Die Standardabweichung wird öfter verwendet als die Varianz, da man sie besser deuten kann (siehe Praxisbeispiel unten).

Die Standardabweichung ist ein Maß, dass aufzeigt wie weit die einzelnen Werte um den Erwartungswert verstreut sind, d.h. wenn die Werte weit auseinander liegen, ist die Standardabweichung groß, liegen sie nah beieinander, ist die Standardabweichung klein.

Wo kommt die Standardabweichung vor?

Wie oben erwähnt, zeigt die Standardabweichung an, ob Werte sich stark unterscheiden. Der Erwartungswert ist z.B. nicht aussagekräftig, falls die Standardabweichung zu groß beim berechneten Erwartungswert pro Jahr von Rohstoffen ausfällt. Man sollte in diesem Fall überlegen, ob man nicht einen kleineren Zeitintervall für den Erwartungswert nimmt (z.B. pro Halbjahr oder Monat).

Wie wird die Varianz und Standardabweichung berechnet?

Die Varianz wird mit Var(X) bezeichnet und die Standardabweichung mit den kleinen griechischen Buchstaben σ (Sigma).

Deshalb sieht die Formel für die Varianz folgendermaßen aus:

Bei dieser Formel werden zunächst die einzelnen Werte (xi) vom Erwartungswert (E(X)) abgezogen. Die Ergebnisse daraus werden quadriert und zusammengezählt, dann durch die Anzahl der Daten (N) geteilt.
Die Standardabweichung ist die Wurzel der Varianz.

Formel der Standardabweichung:

Praxisbeispiel zur Varianz und Standardabweichung

Excel hat auch für die Varianz eine Formel: VAR.P
und für die Standardabweichung: STABW.N

Zurück zu unserem Ölpreisbeispiel. Ich habe hier die Varianz und die Standardabweichung jeweils für 2014 und für den gesamten Zeitraum vom Januar 2014 – Mai 2015.

Man sieht auf den ersten Blick, dass man bei der Varianz zwar einen Unterschied feststellt, dieser aber schwer einzuschätzen ist. Die Standardabweichung beträgt für das Jahr 2014 10,69. Das heißt, dass die meisten Abweichungen vom Erwartungswert in einem Bereich von +/-10 Barrel um den Erwartungswert liegen.

Die Standardabweichung im gesamten Zeitraum beträgt stolze 21,3. Dies ist die doppelte Abweichung, was daran liegt, dass die Werte im gesamten Zeitraum noch weiter auseinander liegen.

Praxisbeispiele für Statistik im Kleinunternehmen

Ein Beispiel für die Statistik im Kleinunternehmen ist daher die optimierte Bestellung von Rohstoffen.

Man kann den Erwartungswert für die Bestellungen pro Jahr errechnen und somit feststellen, ob man Bestellungen bündeln kann. Auf diese Weise können Versandkosten gespart werden oder dementsprechend saisonal abhängige Preise genutzt werden.

Zusätzlich kann man die Preisschwankungen pro Monat festhalten, und dies dann in ein Diagramm übertragen. Damit wird deutlich, in welchen Monaten man einen Rohstoff zu einen niedrigeren Preis erhält. Lieferungen für das nächste Jahr werden besser planbar.

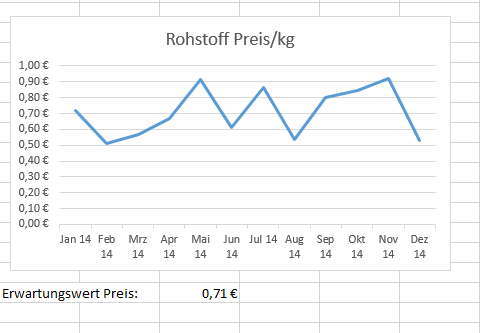
Hier sieht man ein Beispiel für eine Rohstoffbestellung mit Zufallszahlen, und es wurden Erwartungswert und Standardabweichung von der bestellten Menge gebildet.

Der Erwartungswert zeigt, dass wir durchschnittlich pro Monat 515,50 kg Rohstoffe kaufen. Die Standardabweichung ist äußerst hoch mit 298,21.

In diesen Fall bedeutet es, dass wir unregelmäßig bestellen und bei den Bestellungen große Mengenunterschiede haben. Diese Statistik zeigt, dass es sinnvoll wäre mehrere Bestellungen zusammenzufassen, vor allem wenn man den stark schwankenden Preis betrachtet.

In diesen Diagramm sieht man die Preisschwankungen. Zusätzlich wurde der Erwartungswert des Preises berechnet, dieser liegt bei 0,71€.

Man sollte darauf achten, in welchen Monaten der Preis unter dem Erwartungswert liegt (Januar bis April), um eine größere Bestellung aufzugeben. Wenn man den Bedarf pro Monat einbezieht, kann man sich einen optimalen Plan erstellen, wann man wieviel bestellt.

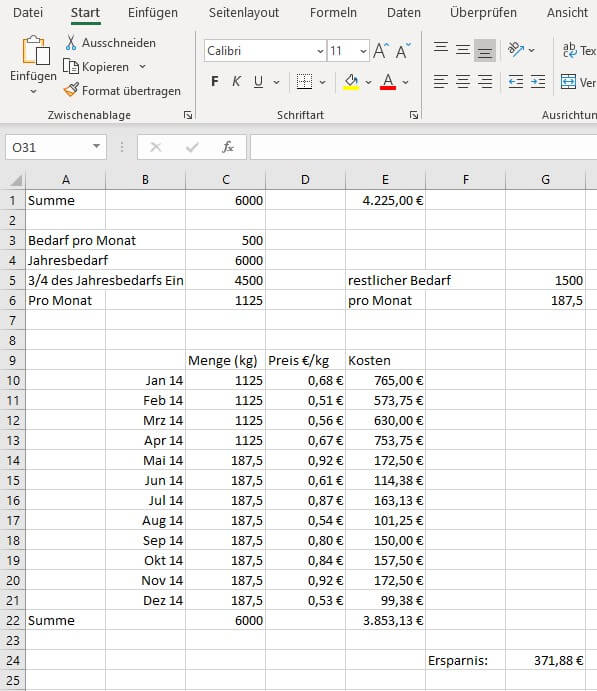
Beispiel für die Berechnung:

Annahme: Pro Monat gibt es einen durchschnittlichen Verbrauch von 500 kg.

Bestellt man den Großteil in dem niedrigpreisigen Zeitraum von Januar bis April, zum Beispiel ¾ der Bestellungen, gilt:
Jahresbedarf = 500 kg*12 Monate
¾ vom Jahresbedarf sind 4500 kg.
Durch effiziente Planung zahlt man für die gleiche Menge von Rohstoffen (6000 kg) 371,88 € weniger.

Was kostet es mich, mit Statistik zu beschäftigen und was bringt es mir?

Diese kleinen statistischen Bewertungsverfahren sind nicht schwierig zu erlernen, vor allem weil uns Software wie Excel die größte Arbeit abnimmt.

Man braucht nur die Daten in eine Excel-Tabelle einzupflegen und ein paar Formeln zu beherrschen. Dadurch kann man viele wirtschaftliche Kenngrößen errechnen. Der größte Aufwand ist es diese Daten aufzuschreiben und in sauberer Form in Excel-Tabellen zu speichern.

Es ist hilfreich den Überblick über diese Daten zu behalten, da sie viel über Ihr Unternehmen aussagen. Wenn man die Lagerhaltungskosten betrachtet und seine Bestellungen und Lieferungen gut plant, kann man Kosten sparen, v.a.durch bessere Rabatte bei größeren Abnahmemengen. Hier macht z.B. die Kombination mit der ABC Analyse Sinn.

Zudem ist es gut zu wissen, wie man im Vergleich zu gleichartigen Unternehmen dasteht. Diese Vorteile rechtfertigen den Arbeitsaufwand, der durch diese statistischen  Analysen entsteht. Je besser Sie Ihr Unternehmen kennen, desto effizienter können Sie handeln. Messen Sie Ihre Prozesse, Ihre Zeiten und Ihren Erfolg mit den richtigen Metoden!

Zusammenfassung und Ausblick

Ich hoffe, dass ich Ihnen einen ersten Einblick in die Statistik geben konnte! Wenn Sie jetzt eine Vorstellung haben, wie Ihnen Statistiken in Ihrem Unternehmen helfen können und wie diese anzuwenden sind, freut mich das!

Dieser Text beinhaltet nur einen kleinen Einblick in die Statistik mit Varianz und Standardabweichung, weitere statistische Themen wären Quantile, Wahrscheinlichkeitsberechnungen und damit verbundene Vorhersagen über die Weiterentwicklung  der Daten.

Diese Themen erfordern jedoch einen genaueren Einblick in die Mathematik und sind schwierig zu behandeln. Außerdem erfordern diese Teilbereiche der Stochastik normalerweise größere Datensätze, was für kleinere Unternehmen ein zu großer Aufwand für zuwenig Nutzen wäre.

Besten Gruß aus Bayreuth
Axel Schröder

Bildquelle: fotolia, © contrastwerkstatt
Die Daten der Ölpreisentwicklung stammen von der Website:
https://www.getoil.de/oelpreisprognose-und-oelpreisentwicklung/

Standardabweichung, Varianz & Co jetzt mit Excel-Tabelle berechnen!

In unserer Excel-Tabelle finden Sie alle wichtigen Formeln, um die verschiedenen Berechnungen selbst durchzuführen.